Aprendizaje supervisado
Introducción
El aprendizaje supervisado tiene como objetivo predecir un valor o la pertenencia a una categoría, basándose en una amplia variedad de algoritmos dedicados. El propósito de este capítulo es conocer estas diferentes familias de algoritmos y ponerlas en práctica en un ejemplo completo de regresión y después de clasificación.
Las familias de algoritmos
Hemos visto anteriormente que los algoritmos de Scikit-Learn están bien identificados según su propósito: los algoritmos dedicados a la regresión tienen todos un nombre que termina en Regressor, y los dedicados a la clasificación tienen todos un nombre que termina en Classifier.
Vamos a ir más allá de esta noción de destino para fijarnos en el espíritu de cada algoritmo, independientemente de su finalidad. Será la ocasión de conocer mejor las características de cada uno y utilizarlos de manera más adecuada.
Nuestro enfoque se dividirá en tres familias principales: algoritmos lineales, semilineales y no lineales. Hablaremos de cada una de las principales familias de algoritmos, de cómo instalarlos y de los parámetros externos que hay que ajustar para optimizar su rendimiento. Estos parámetros externos se denominan hiperparámetros.
1. Los algoritmos lineales
Los algoritmos lineales buscan básicamente establecer una relación lineal entre las características y una variable objetivo. Este tipo de enlace, que es bastante simple, está destinado a explicar sistemas menos complejos. Por tanto, se trata de opciones que hay que aplicar de manera prioritaria; que reflejarán, en función de los resultados, la complejidad del sistema y servirán de referencia para comparar el rendimiento de algoritmos que gestionan relaciones más complejas. Conozcamos a los miembros de esta familia.
a. Las regresiones
La regresión lineal y la regresión logística son técnicas lineales en las que se supone que el efecto de las variables independientes sobre la variable objetivo es aditivo y proporcional. Son los únicos algoritmos de Scikit-Learn cuyos nombres no terminan en Regressor o Classifier, aunque representan a cada uno de estos casos, respectivamente. Antes de pasar al estudio específico de cada una de ellas, hay que tener en cuenta que puede haber una o varias variables explicativas. En el caso de una sola, estamos hablando de una regresión simple, donde se ajustará una línea a los puntos. Si hay varias, se denominará regresión múltiple, donde se ajustará un hiperplano a los datos.
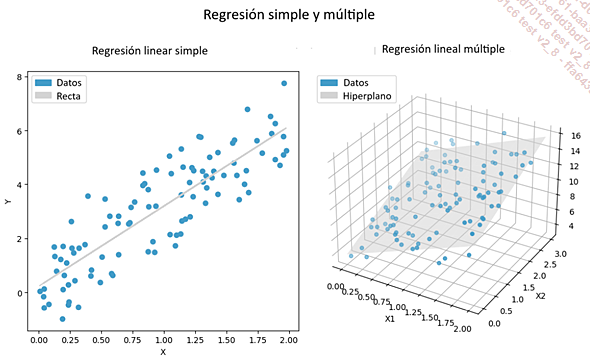
La regresión lineal
La regresión lineal, mostrada en sus versiones simple y múltiple...
La regresión en la práctica
Se utilizará aquí el conjunto de datos de los diamantes para experimentar con los pasos de un modelo de regresión. Este juego cuenta con 53 940 observaciones sobre diferentes características de los diamantes, como los quilates, el tamaño, el color, las dimensiones o el precio. Nos gustaría predecir el precio de un diamante a partir de la tabla (ancho de la parte superior del diamante en relación con el punto más ancho), el número de quilates y su color.
Se ha realizado previamente un trabajo de ingeniería de características, por lo que algunas variables se seleccionarán directamente o se ignorarán en nuestro ejemplo. El objetivo aquí es centrarse solo en el modelado.
1. Preparación de los datos
a. Importación de los datos
Comenzamos con la importación de los datos, teniendo cuidado de eliminar las observaciones con dimensiones nulas o extremadamente altas. Esta supresión solo afecta a 23 observaciones.
import seaborn as sns
df_brut = sns.load_dataset("diamonds")
# Conservación de las medidas válidas y no aberrantes
condition = 'x != 0 and 0 < y < 30 and 0 < z < 30'
df = df_brut.query(condition).reset_index(drop=True)
df.head() 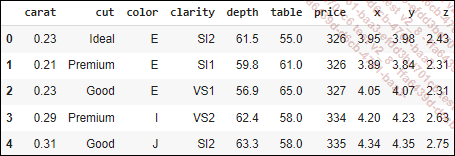
Antes de continuar, veamos la distribución de la variable price:
# Boxplot de price
sns.boxplot(x=df['price'],color="#439CC8", width=0.5)
plt.title("Diagrama de cajas de los precios de los diamantes\n")
plt.show() 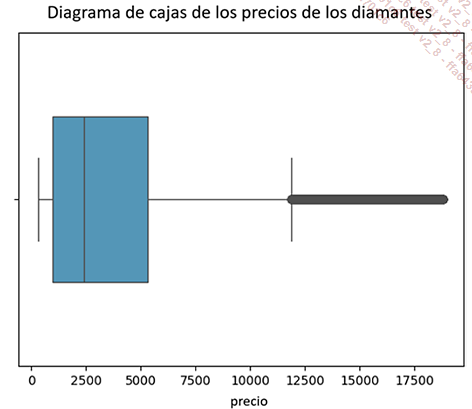
Los precios de los diamantes oscilan entre los 326 y los 18 823 euros, con un precio mediana de 2401 y un precio medio de unos 3931 euros.
b. Separación de las variables explicativas de la variable objetivo
La primera medida después de la importación consistirá en separar las variables explicativas de la variable que se ha de explicar, colocándolas en dos tablas X e y diferentes.
X = df[["table","carat","color"]] # Variables explicativas
y = df["price"] # Variable objetivo c. Separación de los datos de entrenamiento y de prueba...
La clasificación en la práctica
Ahora vamos a practicar una clasificación. Para ello, tomaremos el ejemplo de los «diamantes» tratando de deducir la calidad del corte del diamante a partir de otras variables.
1. Preparación de los datos
a. Importación de los datos
Comencemos importando los datos y eliminando directamente las medidas inexistentes o atípicas:
import seaborn as sns
import pandas as pd
import numpy as np
# Importar el juego de datos
df = sns.load_dataset("diamonds")
# Eliminar las medidas inexistentes o aberrantes
df = df_brut.query('x != 0 and 0 < y < 30 and 0 < z < 30')
.reset_index(drop=True) b. Separación entre las variables explicativas y la variable objetivo
A continuación, prepararemos las matrices X e Y. Asegúrese aquí de pasar la matriz y de tipo category:
# Preparación de las matrices X y y
X = df[["price","table","depth","color","clarity"]]
y = pd.Series(df['cut'], dtype='category') c. Separación de los datos de entrenamiento y de prueba
La separación entre los datos de entrenamiento y de prueba se lleva a cabo de la siguiente manera:
from sklearn.model_selection import train_test_split
# División de los datos entre entrenamiento y prueba
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=42, stratify=y) El uso de stratify en la función train_test_split permite mantener las proporciones de las clases entre los conjuntos de entrenamiento y prueba
d. Transformación de columnas
Una vez que los datos están separados, vamos a transformarlos de una manera específica en función de su tipo, usando la función ColumnTransformer. Después de diseñar las variables numéricas y categóricas, aplicaremos una estandarización para las primeras y una binarización para las segundas, respectivamente:
from sklearn.compose import ColumnTransformer
# Identificación de las columnas numéricas y binarias
numeric_columns = X.select_dtypes(include=['number']).columns
categorical_columns...Conclusión
En conclusión, este capítulo ha presentado los fundamentos del modelado supervisado en regresión y clasificación. Hemos cubierto los conceptos esenciales y omitido ciertas nociones para evitar la sobrecarga de información. Es importante subrayar, a este respecto, que la gama de herramientas y técnicas disponibles es abundante y, a veces, compleja.
Para dominar realmente estos métodos, es esencial la práctica regular. Profundizando en nuestra comprensión y aplicando estas técnicas en distintos ámbitos, podremos refinar nuestros análisis, ampliar nuestra caja de herramientas y desarrollar habilidades más avanzadas.
La tabla siguiente es un resumen de los experimentos comentados:
|
Aspecto |
Regresión |
Clasificación |
|
Variable objetivo |
Variable continua (cuantitativa) |
Variable discreta (categórica) |
|
Evaluación del rendimiento |
Error cuadrático medio (MSE), error absoluto medio (MAE), R² |
Matriz de confusión, Accuracy, Precisión, Recuperación, F-score |
|
Hipótesis del modelo |
Relación lineal o no lineal, independencia de observaciones y variables |
|
|
Preprocesamiento de datos |
Normalización/estandarización de variables Detección de valores atípicos Codificación de variables categóricas Modificación del tipo |
|
|
Elección de las variables |
Selección basada... | |
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática