Análisis de datos
Introducción al análisis de datos
1. Definición y función del análisis de datos
Como parte del análisis exploratorio de datos (comúnmente conocido como EDA, de Exploratory Data Analysis), la exploración y el análisis trabajan en conjunto para profundizar nuestra comprensión de la información, visible u oculta, que revelan los datos. Si bien la exploración nos permite echar un primer vistazo e identificar los patrones iniciales, el análisis hace posible perfeccionar este conocimiento a través de un examen más cuidadoso gracias, en particular, a las herramientas estadísticas que permiten medir los fenómenos observados y validar si se pueden considerar significativos o no.
Tomemos el ejemplo de un rompecabezas: si la exploración nos permitiera entrever, a través del examen de las formas y de los colores, la posibilidad de ensamblar ciertas piezas, el análisis representaría el examen minucioso que confirmaría la viabilidad de los distintos ensamblajes.

2. Desafíos
Las pruebas estadísticas y los métodos de análisis exploratorio son esenciales en el estudio de los datos. Gracias a los nuevos conocimientos que aportan, tendremos la oportunidad de innovar, de tomar conciencia de las limitaciones y de mejorar la toma de decisiones.
a. Innovación y creatividad
El suministro de nueva información, ilustrada de tres maneras diferentes y que se describe a continuación, fomentará el surgimiento de la innovación y la creatividad. Este conocimiento profundo de los datos nos permitirá diseñar soluciones originales.
Identificación de características importantes
En primer lugar, el análisis permite identificar los elementos que tienen un impacto significativo en el campo estudiado. Esto nos permitirá identificar variables de interés, comprender los vínculos entre ellas y priorizar acciones para ellas. A la hora de analizar las ventas de un restaurante...
Estadísticas descriptivas e inferenciales
El análisis de variables requiere una revisión de ciertos conceptos estadísticos. No se trata de ahogarse en detalles, sino simplemente de comprender las principales herramientas necesarias para el análisis.
El análisis estadístico se basa en dos pilares, la estadística descriptiva y la estadística inferencial, cada una de las cuales desempeña un papel muy específico.
El propósito de la estadística descriptiva es describir y resumir un conjunto de datos de la mejor manera posible. Para facilitar la comprensión y la aplicación de los conceptos, estudiaremos las medidas para las variables cuantitativas y categóricas por separado. Este enfoque permitirá distinguir los métodos específicos de cada tipo de variable.
La estadística inferencial permite generalizar las características de una muestra de datos a una población general, con el fin de hacer predicciones. Utilizaremos pruebas específicas para cada tipo de caso que validarán o no nuestras hipótesis.
Antes de conocer las diferentes estadísticas, es útil definir la noción de robustez, de la que se hablará en profundidad. Se dice que una prueba o medición es robusta si proporciona resultados fiables y precisos, incluso cuando no se cumplen todas las condiciones ideales. Estas son las situaciones que una prueba o medición robusta debe ser capaz de manejar:
-
la presencia de valores atípicos,
-
la no normalidad de la distribución,
-
los datos ordinales,
-
los ex aequo.
Esta robustez es esencial para garantizar conclusiones válidas en condiciones diversas.
1. Descripción de las variables cuantitativas
El examen de las variables cuantitativas, también llamadas variables continuas, se lleva a cabo en tres etapas: identificar el centro, describir la variabilidad alrededor de este centro y analizar de manera más general la distribución de los valores de la variable.
a. Medidas de tendencia central
La medida de tendencia central se basa principalmente en tres herramientas: la media, la mediana y la moda. Lo que tienen en común es que son fáciles de construir y entender.
La media
La media aritmética es una de las herramientas más utilizadas. Consiste en sumar todos los valores y dividirlos...
Módulos de Python para el análisis de datos
Antes de elegir y de poner en práctica las diversas pruebas estadísticas, es conveniente hacer un balance de las posibilidades que ofrecen las librerías de Python en este ámbito.
1. Las capacidades limitadas de los módulos convencionales
Las librerías tradicionales, como Pandas o NumPy, ofrecen, además de sus funciones de manipulación de datos, algunas funciones de cálculo de indicadores estadísticos. Estas capacidades se limitan a la estadística descriptiva y a la capacidad de calcular la correlación y la covarianza. Aunque algunas ya se han comentado anteriormente, he aquí una tabla resumen que sintetiza sus posibilidades:
|
Función |
Pandas |
NumPy |
|
Media |
|
|
|
Mediana |
|
|
|
Moda |
|
No disponible |
|
Desviación típica |
|
|
|
Varianza |
|
|
|
Mínimo |
|
|
|
Máximo |
|
|
|
Resumen estadístico |
|
No disponible |
|
Percentiles |
|
|
|
Cuantiles |
|
|
|
Asimetría |
|
No disponible |
|
Aplanamiento |
|
Pruebas estadísticas de normalidad
1. Contexto y objetivo
Las pruebas de normalidad de distribución son un paso fundamental en el análisis de datos, especialmente para variables numéricas. Su objetivo es determinar si la distribución de una variable sigue una distribución típica. Esta verificación es esencial porque influye en la elección de los métodos estadísticos que se aplicarán en el futuro, con el fin de determinar si existe una relación entre las variables. En efecto, la normalidad de una variable condiciona el uso de pruebas paramétricas, que suponen una distribución típica de los datos, o pruebas no paramétricas, que son más adecuadas cuando no se cumple esta condición.
Antes de pasar a la prueba propiamente dicha, vale la pena presentar los gráficos cuantil-cuantiles (Q-Q Plots) que ofrecen una forma intuitiva y visual de representar la normalidad de los datos.
2. Los Q-Q plots
a. Definición y trazado del gráfico
Los Q-Q plots (QQ por Quantile-Quantile) son gráficos que comparan los cuantiles de un conjunto de datos con los cuantiles de una distribución teórica, a menudo la distribución típica. Al trazar los cuantiles observados y los cuantiles teóricos, podemos ver fácilmente si nuestros datos parecen estar distribuidos normalmente o no.
Pongamos un ejemplo que comentaremos para entender cómo utilizar este tipo de visualización:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import scipy.stats as stats
# Importar el juego de datos de los iris
iris = sns.load_dataset("iris")
# Seleccionar una columna numérica
data = iris['sepal_length']
# Crear un Q-Q plot
plt.figure(figsize=(5, 3))
stats.probplot(data, dist= »norm », plot=plt)
# Modificar el color...Pruebas estadísticas bivariantes
Las pruebas estadísticas bivariantes examinan la relación entre dos variables para identificar asociaciones o diferencias significativas, lo que ayuda a comprender los posibles vínculos y formular hipótesis de investigación que faciliten la toma de decisiones. También proporcionan una base para análisis más complejos, como la regresión y los modelos multivariantes.
Seguiremos este diagrama para estudiarlas, comenzando por las pruebas aplicadas a dos variables de la misma naturaleza, y después a dos variables de naturaleza diferente.
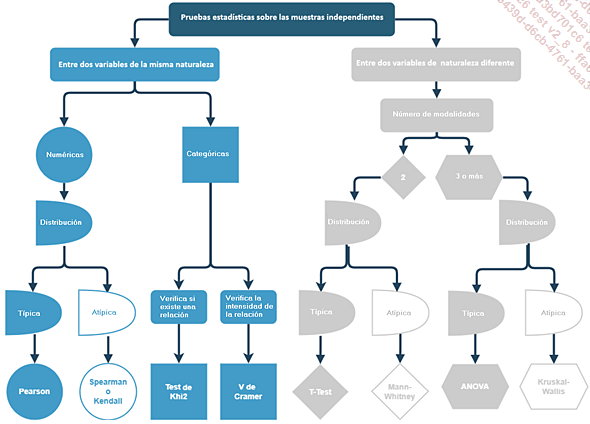
Nos centraremos en probar muestras independientes, es decir, grupos que están completamente separados entre sí. Conviene señalar que también hay pruebas en grupos emparejados que se centran en el mismo grupo, donde cada observación se asocia a una observación correspondiente en otro grupo. Este es el caso, por ejemplo, de un grupo antes y después de un tratamiento médico. Para no ahogarse en información, este caso se omitirá, pero una simple búsqueda facilitará encontrar la prueba correcta.
1. Pruebas bivariantes entre variables de la misma naturaleza
a. Correlaciones entre variables numéricas
Principio y desafíos de la correlación
Comencemos esta familiarización con las pruebas bivariantes con correlaciones de tipo lineal, es decir, cuando la relación entre dos variables se puede describir mediante una línea recta.
Estas pruebas entre dos variables numéricas son esenciales porque nos permiten medir, entre -1 y 1, la fuerza del vínculo entre las dos variables. Una correlación de 1 indica una relación perfectamente positiva, -1 indica una relación perfectamente negativa y 0 ninguna relación en absoluto. Por lo tanto, las correlaciones son esenciales para identificar y cuantificar las posibles relaciones lineales entre las variables y, a menudo, se visualizan utilizando matrices de correlación o diagramas de dispersión.
He aquí un diagrama ilustrativo que muestra el coeficiente de correlación para diferentes relaciones entre dos variables:
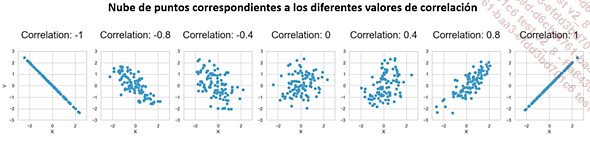
También hay pruebas para relaciones no lineales que cubriremos a continuación, con la correlación de Spearman y el tau de Kendall.
El uso de la correlación...
Análisis multivariante
El objetivo del análisis multivariante es examinar múltiples variables simultáneamente para comprender las complejas relaciones e interacciones que existen entre ellas. Ayuda a revelar patrones ocultos y proporciona una visión general coherente de cómo funciona un conjunto de datos en general. Este es un paso esencial que finaliza el análisis de los datos y nos permite identificar con certeza las variables más importantes y las leyes que rigen el conjunto de datos estudiado.
Antes de entrar en el Análisis de Componentes Principales (ACP), que es un pilar fundamental del análisis multivariante, exploraremos otras dos técnicas que satisfacen necesidades específicas: el análisis multivariante de varianza (MANOVA) y el Análisis de Correspondencias Múltiples (ACM).
1. Análisis de la varianza multivariante (MANOVA)
a. Presentación y campos de aplicación
MANOVA es una generalización de ANOVA que tiene como objetivo determinar si una o más variables categóricas están relacionadas con las medias de varias variables numéricas dependientes. Resulta particularmente útil para evaluar los efectos combinados de varios factores y comprender mejor las complejas relaciones entre diversas variables.
b. Caso de práctico de uso
Tomemos el conjunto de datos de diamantes proporcionado por Seaborn:
import seaborn as sns
df = sns.load_dataset("diamonds")
df.head() 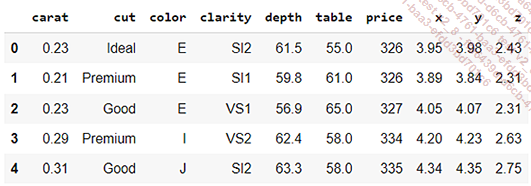
Sería interesante saber si las variables cualitativas que describen el corte y el color tienen un impacto en variables numéricas como los quilates y el precio. Esta es una oportunidad para implementar una MANOVA utilizando el módulo statsmodels:
from statsmodels.multivariate.manova import MANOVA
# Fórmula para MANOVA
formula = 'carat + price ~ cut + color'
# Ajuste del modelo MANOVA
manova = MANOVA.from_formula(formula, data=df)
result = manova.mv_test()
# Visualización de los resultados
print(result) 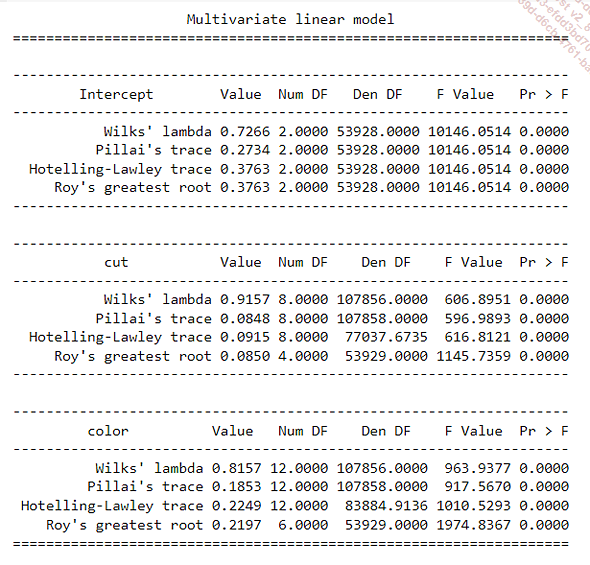
El algoritmo MANOVA utiliza diferentes pruebas para validar o no los enlaces. En nuestro caso, la constante (Intercept), así como las dos variables categóricas, tienen un vínculo significativo...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática