En torno a los datos

Captura directa y rápida de un dataset

Para evitar redundancias innecesarias, vamos a equiparnos con un dataset cuyos datos se utilizarán en el capítulo, que trata sobre la creación de un modelo sin programación usando una herramienta como BigML. El paquete mlbench permite acceder a estos datos y también construir datasets adaptados a un tipo de problema.

library(tidyverse) 
library(mlbench)      # paquete para crear o acceder a los datos de prueba 

Puede enumerar fácilmente todos los datasets de demostración que se ofrecen en los paquetes instalados en una máquina.

data(package = .packages(all.available = TRUE)) # lista de los datasets disponibles 

A continuación, se muestra un (muy) breve extracto de lo que está disponible en nuestra máquina:

... 
Data sets in package ‘mlbench': 
 
BostonHousing            Boston Housing Data 
BreastCancer             Wisconsin Breast Cancer Database 
DNA                      Primate splice-junction gene sequences (DNA) 
Glass                    Glass Identification Database 
HouseVotes84             United States Congressional Voting Records 1984 
Ionosphere               Johns Hopkins University Ionosphere database 
LetterRecognition        Letter Image Recognition Data 
Ozone                    Los Angeles ozone pollution data, 1976 
PimaIndiansDiabetes      Pima Indians Diabetes Database 
... 

Vamos a invocar los siguientes datos:

data(PimaIndiansDiabetes)  # acceso a los datos de diabetes de los indios 
df <- data.frame(PimaIndiansDiabetes) 

Contiene información sobre la diabetes de las mujeres de una tribu india de América del Norte (los Pimas...

Análisis de la conformación de las distribuciones respecto a la distribución normal

Podemos validar algunas de nuestras intuiciones respecto a la normalidad de los datos comparando estas densidades con la ley o distribución normal mediante un diagrama Cuantil-Cuantil.

# ajustes de la ley normal (mu,e) 
plot_qq(df)          # diagramas Cuantil-Cuantil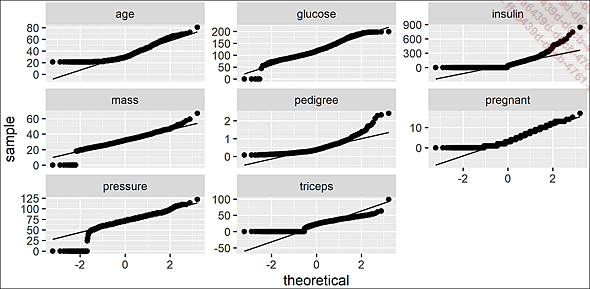 

Diagramas Cuantil-Cuantil

Incluso sin saber cómo interpretar con precisión un diagrama de este tipo, llama nuestra atención sobre ciertas características de los datos:

Este ajuste se puede comparar distinguiendo entre los casos «con» o «sin» diabetes.

# comparando...

Dependencia lineal entre variables

De forma adicional, es habitual comprobar si algunas de las variables explicativas no están fuertemente correlacionadas, lo que podría provocar que se prueben modelos de predicción que mantendrían solo una u otra de estas variables (para hacerlo bien, comparamos la eficiencia con ambas y, cuando es similar, nos quedamos con la variable que es más fácil de interpretar o recopilar en el mundo real).

plot_correlation(df) # una tabla de correlaciones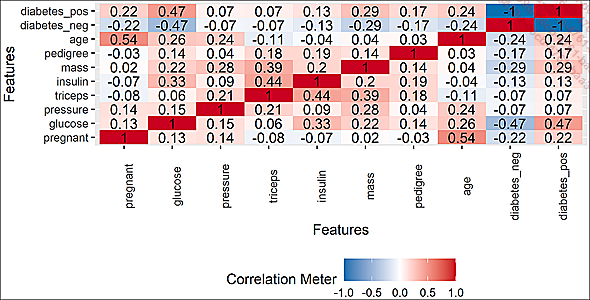 

Correlación dos a dos

Nuestro problema no es linealmente trivial; de forma clara, la diabetes no se correlacionada solo con una variable. Exceptuando la variable age, parece completamente descartado que exista alguna relación más o menos lineal y simple entre el número de embarazos y el resto de las variables explicativas. Podemos representar esto, quizás erróneamente, imaginado dos grandes familias de predictores: «sociales» (edad, número de embarazos) y técnicos (el resto). Dicho todo esto, tenga en cuenta que esta pista solo se ocupa de las relaciones lineales, que no es el caso más común en la realidad. Recordemos también que la calidad de los predictores no nos permite sacar conclusiones sobre la noción de causalidad.

Ahora bien: nada nos impide formarnos una opinión personal sobre la monotonía de la relación entre dos variables...

Resalte de las diferencias entre las distribuciones

Ahora intentaremos resaltar (o no) las posibles diferencias en las distribuciones para ciertas variables de aspecto gaussiano (para este ejemplo, hemos elegido glucose) entre la distribución con diabetes o sin ella.

Nuestra principal preocupación será la importancia de cualquier diferencia en la media. La herramienta también nos aporta información sobre la diferencia en la desviación típica, que no requiere una interpretación fuerte, sino que el hecho de que sea significativa puede reforzar la idea de que un algoritmo bien elegido podrá mejorar la predictibilidad de diabetes

library(lessR) 
d <- df                         # por defecto lessR utiliza d como dataset 
tt.brief(glucose ~ diabetes)   # gráfico y estados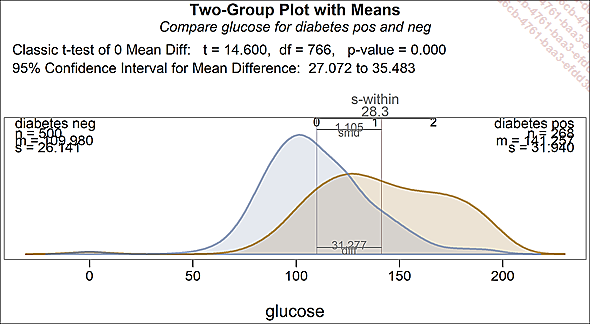 

Distribuciones de la glucosa en función de la diabetes

La diferencia en la media es significativa

También es posible que desee una representación de «bigote/violín», utilizando la siguiente sintaxis:

library(ggstatsplot) 
 
set.seed(666) 
ggbetweenstats( 
 data = df, 
 x = diabetes, 
 y = glucose, 
 title = "Distribución de la glucosa con o sin diabetes" 
) 

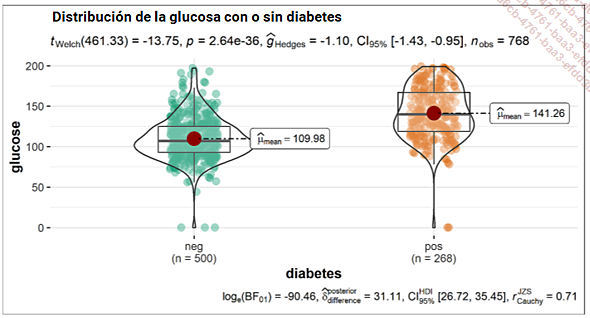
Diagrama de bigotes/violín comparado

También podemos...

Puntos atípicos

Ya hemos trabajado en la identificación de valores atípicos u outliers. La siguiente representación permitirá extraer observaciones candidatas para calificarlas como puntos atípicos. Mediante pruebas sucesivas de diferentes parámetros, puede evaluar el mayor o menor poder de discriminación del contorno que va a dibujar. Falta por estudiar de manera individualizada los puntos exteriores, cuyo identificador está especificado, para comenzar a vislumbrar su estrategia de tratamiento de este tipo de puntos.

Mantener puntos técnicamente atípicos u extraños (ya sean anomalías o no) se puede considerar válido o no, dependiendo del tratamiento que se aplique a estos valores. Mantener o no los puntos correspondientes a observaciones excepcionales puede ayudarlo a reducir el overfitting o, por el contrario, disminuir la predictibilidad de sus modelos. Cualquier decisión de este tipo se debe registrar cuidadosamente como una hipótesis estructurante en la documentación de sus modelos. A menudo tendrá que verificar estas suposiciones y cambiar su posición sobre ellas para mejorar su trabajo. No tome al pie de la letra las afirmaciones que pueda encontrar por ahí, aunque parezca que le proporcionan un método automático para manejar los valores outliers (lo que no le impide crear un método y automatismos...

Ordenaciones y agregaciones

# una pequeña función para imprimir head + tail de un objeto dato 
h_t <- function(x, titulo = "", sub_titulo ="", n = 3) 
         { 
          cat(titulo, "\n") 
          cat(sub_titulo, "\n") 
          print(rbind(head(x,n),tail(x,n))) 
         } 

# ordenación plana sobre 2 var discretas 
t <- table(df$pregnant,df$diabetes)             # ordenación sencilla 
h_t(t, 
   "6 líneas extraídas de una simple ordenación plana, núm embarazos 
vs estado respecto a la diabetes", 
   "----------" 
   ) 
 
6 líneas extraídas de una simple ordenación plana, núm embarazos vs 
estado respecto a la diabetes 
---------- 
  neg pos 
0   73  38 
1  106  29 
2   84  19 
14   0   2 
15   0   1 
17   0   1 

t <- addmargins(table(df$pregnant,df$diabetes)) # ordenación con las sumas 

6 líneas extraídas de una simple ordenación plana, núm embarazos vs estado respecto a la diabetes 
--------------- 
   neg pos Sum 
0    73  38 111 ...