Los gráficos para ayudar en el cálculo
Introducción
Los ejemplos de este capítulo están distribuidos en cuatro hojas en la carpeta descargable de Excel: Capítulo 10a, Capítulo 10b, Capítulo 10c y Capítulo 10d.
A pesar de que este programa no esté especializado en este dominio, Excel permite el trazado de curvas, que se trata de un ámbito importante en las matemáticas clásicas. Las curvas son una de las categorías gráficas que Excel puede realizar.
Para crear este tipo de gráfico:
Seleccione el rango de celdas que contenga los datos; para nuestro ejemplo, el rango A1:B102.
En la pestaña Insertar, grupo Gráficos, haga clic en el botón 
El trazado de curvas
Las curvas y=f(x)
Escriba en una primera columna una serie de valores de x, regularmente espaciados o no. Calcule en la columna adyacente a la derecha los valores de f(x) correspondientes.
¡Atención! Hay que suprimir los valores de f(x) demasiado altos con respecto a los valores extremos escogidos para x; en caso contrario tendremos un gráfico ilegible.
Ejemplo:
Trazado de la curva y=1/x (la hipérbola)
Realización con Excel:
Escriba en la columna A una serie de valores de x entre -5 y +5 a intervalos de 0,1.
Calcule los valores correspondientes de 1/x en la columna B.
Borre las celdas con valores demasiado grandes, es decir, el rango A51:B53.
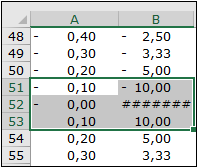
Seleccione el rango de celdas A1:B102.
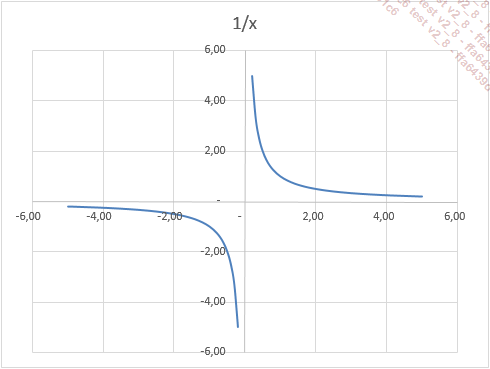
Escoja el tipo de gráfico "X Y (Dispersión) con líneas rectas".
Por lo tanto el gráfico muestra la imagen clásica de la hipérbola.
Las curvas en coordenadas polares ρ=f(θ)
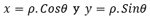 .
.Ejemplo 1:
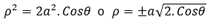 .
.Realización con Excel: para obtener todos los valores de X y de Y, hay que hacer variar θ entre 0 y 360°. Esto permite obtener automáticamente los valores positivos y negativos de ρ pero, al revés obtenemos valores negativos para Cos2θ.
Cuando se da el caso, la función...
El trazado de tangentes
La técnica general del trazado de una tangente
Para obtener el trazado de una tangente, basta con calcular las coordenadas de dos puntos, A y B, de esta recta.
Por lo tanto, el trazado en un gráfico de Excel se obtendrá agregando coordenadas de esos dos puntos en la selección de datos.
La definición exacta de la pendiente de la tangente en el punto M en la curva y=f(x) es:
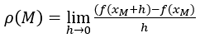
Para el cálculo con Excel, aplicaremos la aproximación:
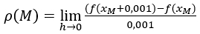
La tangente se limitará a un segmento de recta de longitud l, cuyo centro corresponderá al punto M.
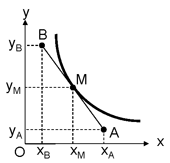
El proceso de cálculo es el siguiente:
Se fija la longitud l del segmento de la tangente.
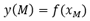 .
.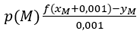 .
.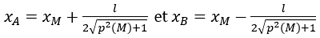 .
.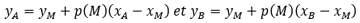 .
.Ejemplo:
Retomemos el caso de la hipérbola que estudiamos en el apartado Las curvas y=f(x).
Realización con Excel:
Escriba la longitud l del segmento de tangente en H1.
Escriba la abscisa xM en H3.
Escriba la ordenada YM en H4.
Escriba la pendiente p(M) en H5.
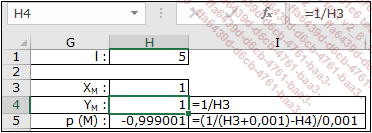
A continuación calcule, con ayuda de las fórmulas anteriores, las coordenadas de los extremos A y B del segmento de tangente en las celdas que se incorporarán a la selección de datos del gráfico.
Separe las coordenadas de estos dos puntos A y B de la serie de puntos de la curva, para eliminar una continuidad inoportuna entre la curva y la tangente.

Modifique la selección de datos del gráfico. Haga clic en la pestaña Herramientas de gráficos...
Las curvas de tendencia
La técnica de la curva de tendencia es útil cuando queremos establecer un modelo de una serie de observaciones para realizar previsiones. Los gráficos Excel permiten agregar fácilmente una curva de tendencia y obtener la ecuación de dicha curva.
Ejemplo:
Se han observado las ventas semanales de un producto nuevo en fase de lanzamiento durante 30 semanas. El objetivo es crear un modelo de esta evolución para prever las ventas en las 10 semanas siguientes.
Empecemos creando un gráfico del tipo de gráfico X Y (Dispersión), subtipo Dispersión. El aspecto del gráfico sugiere una tendencia logarítmica o una tendencia polinomial.
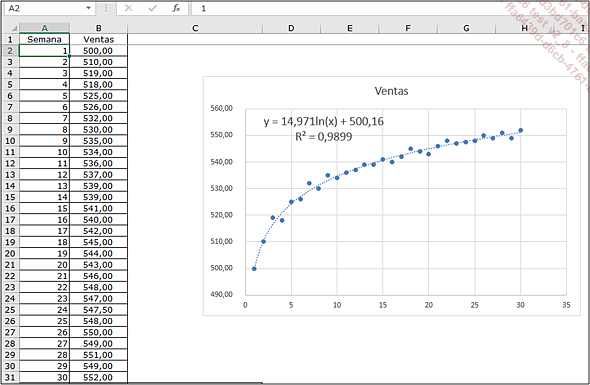
Para agregar una curva de tendencia logarítmica al gráfico:
Haga clic en el gráfico.
Haga clic en la pestaña Herramientas de gráficos - Diseño, grupo Presentación del gráfico, lista desplegable Agregar un elemento de gráfico, escoja Línea de tendencia, Más opciones de la línea de tendencia.
En la ventana a la derecha de la pantalla, marque la opción correspondiente al tipo de línea de tendencia logarítmica. Marque también las opciones Presentar ecuación en el gráfico y Presentar el valor R cuadrado en el gráfico situados en la parte inferior del cuadro de diálogo.
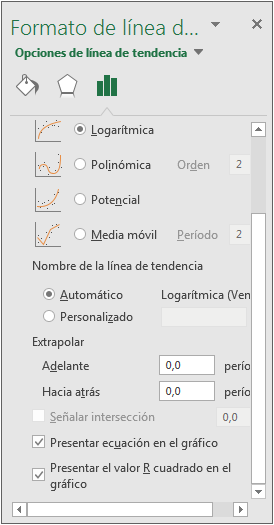
El gráfico se habrá...
Las superficies tridimensionales
Los gráficos de Excel 2016 permiten la representación de superficies tridimensionales (3D). Para ello, hay que emplear la ecuación z = f(x,y) que representa esta superficie.
La entrada de datos se lleva a cabo mediante una tabla Excel rectangular, que consta de una primera columna con los valores de x, una primera fila que representa los valores de y, las celdas que completan el rectángulo son los valores calculados de z mediante la función f(x,y).
Ejemplo1: el paraboloide hiperbólico
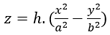
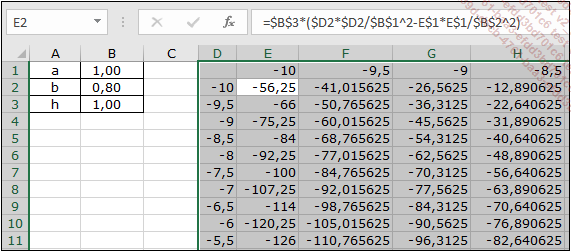
La tabla de datos de Excel se presenta así:
-
Los valores a, b y h se encuentran respectivamente en B1, B2, B3.
-
Los valores de x (-10 a +10 mediante pasos de 0,5) se colocan en el rango D2:D42.
-
Los valores de y (-10 a +10 mediante pasos de 0,5) se colocan en el rango E1:AS1.
La fórmula de base, colocada en E2 y recopiable, que representa el valor de z, es la siguiente: =$B$3*($D2*$D2/$B$1ˆ2-E$1*E$1/$B$2ˆ2)
Seleccione el rango D1:AS42.
Construya el gráfico como se explicó anteriormente, escogiendo el tipo Superficie, subtipo Superficie 3D o Trama de superficie 3D.
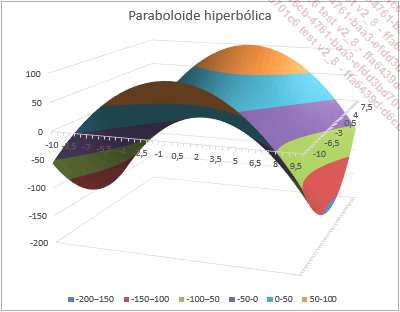
Si pulsa en el ejemplo de la inserción de un slider que se presenta en el párrafo Animar las posiciones de una tangente, el lector podrá aplicar la misma técnica para hacer variar el parámetro b de la ecuación y visualizar...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática