Los cálculos financieros
Las devoluciones de préstamos
En las devoluciones de préstamos entran en juego la cantidad prestada, la duración del préstamo, la tasa de interés aplicada y las modalidades de devolución (a plazo vencido o por vencer). La noción de tasa de interés tiene que precisarse ya que esta representa el precio del dinero.
La tasa de interés de periodo
Por lo general, las tasas de interés se dan refiriéndose a un periodo anual. En la práctica, los flujos de dinero pueden tener cualquier tipo de periodicidad: mensual, trimestral o semestral, por ejemplo. Dichas periodicidades no son neutras.
Pongamos un ejemplo simple: un acreedor presta una cantidad de 10.000 € a una tasa anual nominal del 2,4% que el prestatario se compromete a devolver en un año.
1er caso: el prestatario devuelve al cabo de un año la cantidad de 10.240 € (10.000 + 240 € de intereses). En ese caso, la tasa del periodo es idéntica a la tasa nominal, es decir, 2,4%.
2º caso: por prudencia, el prestamista pide un primer pago de 5.120 € al cabo de 6 meses y los 5.120 € restantes al cabo de un año. Por lo tanto, podemos considerar que el préstamo ha experimentado un coste suplementario debido a que, por ejemplo, va a pedir prestado a otro prestamista esos 5.120 € a una tasa supuestamente idéntica del 2,4%. Esos intereses para ese 2º préstamo serán de: 5.120 x 2,4% x 6/12 = 61,44 €. Finalmente, el prestatario habrá pagado 240+61,44=301,44 € de interés...
Los cálculos de actualización
El valor neto actualizado (flujos periódicos)
El valor neto actualizado es una herramienta que sirve para determinar la rentabilidad de una inversión. Una inversión I realizada en un periodo n=0 generará flujos de tesorerías CFi en los periodos n=1, n=2,…, n=p. Estos flujos de tesorería se ponderan mediante una tasa de actualización ta y mediante el n° del periodo correspondiente al flujo.
La fórmula del valor neto actualizado es la siguiente:
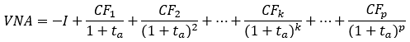
La función Excel VNA calcula el importe global de los valores actualizados de los flujos de tesorería. Por lo tanto, para obtener el Valor Neto Actualizado, hay que quitar la cantidad de la inversión inicial. La sintaxis de la función es la siguiente:
=VNA(tasa de actualización;rango de los flujos)
El ejemplo siguiente muestra una aplicación de la función VNA.
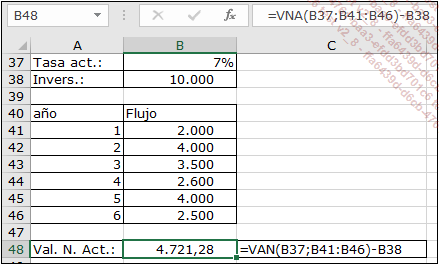
Este cálculo permite deducir que si al valor de la inversión le deducimos el valor net actualizado de los flujos y obtenemos un valor positivo (4.721,28), la inversión se considera rentable.
La tasa interna de rentabilidad (flujos periódicos)
La tasa interna de rentabilidad de una inversión es la tasa correspondiente a un Valor Neto Actualizado igual a 0. Esta tasa se calcula con Excel mediante la función TIR cuya sintaxis es la siguiente:
=TIR(rango de flujos;[tasa estimada])
El rango...
Los cálculos de amortización
La amortización lineal
La amortización lineal consiste en asignar una dotación proporcional en el tiempo a las amortizaciones. Es un cálculo relativamente simple, para el cual la función AMORTIZ.LIN propuesta por Excel no tiene ninguna utilidad.
Ejemplo:
El 1 de julio de 2016 se adquiere una inmovilización de un valor de 10.000 €. La duración de la amortización es de 5 años, es decir, el 20% del valor en un ejercicio completo. Por lo tanto, las dotaciones de las amortizaciones serán las siguientes:
-
2016: 10.000 x 20% x 0,5 = 1.000 (aproximadamente)
-
2017: 2.000
-
2018: 2.000
-
2019: 2.000
-
2020: 2.000
-
2021: 1.000 (el resto)
La tabla Excel siguiente muestra la amortización lineal, sea cual sea la duración de la amortización. Para el primer ejercicio, la duración de la amortización se calcula al día.
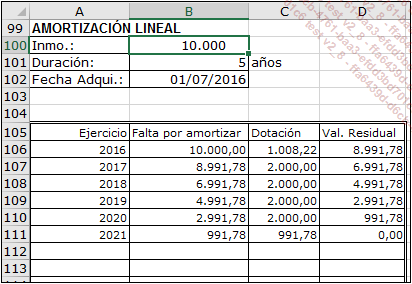
A partir del segundo ejercicio, las líneas de cálculo se pueden reproducir mediante una simple copia para alcanzar la duración máxima de amortización prevista.
Las fórmulas empleadas son las siguientes:
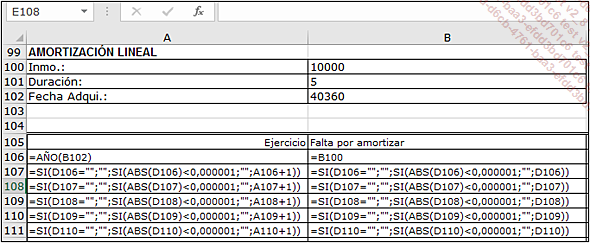
En A106 y B106, las fórmulas son simples.
La fórmula de la columna ejercicio (A), a partir de A107, es la siguiente:
=SI(D106="";"";SI(ABS(D106)<0,000001;"";A106+1))
Esta permite extraer la siguiente lógica: si el valor residual del ejercicio anterior (D106) está vacío, el ejercicio está vacío; si no, si ese mismo valor residual...
 Ediciones ENI Editorial | líder en informática
Ediciones ENI Editorial | líder en informática